Algorithms

title image

背景

简单复习一下最基本的算法和数据结构，可惜一直耽搁了。

部分来自 Introduction to Algorithm 和 https://github.com/keon/algorithms ，还有网络。

1. Sorting

1.1 Quicksort

基本的实现

import random

def quicksort(self, nums):
    if len(nums) <= 1:
        return nums

    pivot = random.choice(nums)
    lt = [v for v in nums if v < pivot]
    eq = [v for v in nums if v == pivot]
    gt = [v for v in nums if v > pivot]

    return self.quicksort(lt) + eq + self.quicksort(gt)

中间存储 O(1) 的实现

def partition(arr, low, high):
    pivot = arr[low]
    i = low - 1
    j = high + 1

    while True:
        i += 1
        while arr[i] < pivot:
            i += 1

        j -= 1
        while arr[j] > pivot:
            j -= 1

        if i >= j:
            return j

        arr[i], arr[j] = arr[j], arr[i]


def quick_sort(arr, low, high):
    if low < high:
        p = partition(arr, low, high)
        quick_sort(arr, low, p)
        quick_sort(arr, p + 1, high)


# Example usage
arr = [10, 7, 8, 9, 1, 5]
quick_sort(arr, 0, len(arr) - 1)
print(arr)  # Output: [1, 5, 7, 8, 9, 10]

1.2 Heapsort

The (binary) heap data structure is an array object that we can view as a nearly complete binary tree (except possibly the lowest)
sort in place
runtime $O(n \lg n)$, height $\Theta(\lg n)$
index of array starts at 1.

  def parent(i):
      return i // 2

  def left(i):
      return 2 * i

  def right(i):
      return 2 * i + 1

  def max_heapify(A, i):
      l = left(i)
      r = right(i)
      if l <= A.heap_size and A[l] > A[i]:
          largest = l
      else:
          largest = i
      if r <= A.heap_size and A[r] > A[largest]:
          largest = r
      if largest != i:
          A[i], A[largest] = A[largest], A[i]
          max_heapify(A, largest)


  def build_max_heap(A):
      A.heap_size = len(A)
      for i in range(len(A) // 2, 0, -1):
          max_heapfiy(A, i)

1.3 Mergesort

计算给定 array 中的 inverse pairs 个数 $O(n\log(n))$

def merge_sort(arr):
    if len(arr) <= 1:
        return arr, 0

    mid = len(arr) // 2
    left, left_inv = merge_sort(arr[:mid])
    right, right_inv = merge_sort(arr[mid:])

    merged, split_inv = merge_and_count(left, right)
    return merged, left_inv + right_inv + split_inv


def merge_and_count(left, right):
    merged = []
    split_inv = 0
    i, j = 0, 0

    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            split_inv += len(left) - i
            j += 1

    merged.extend(left[i:])
    merged.extend(right[j:])

    return merged, split_inv


# Example usage
arr = [5, 3, 2, 4, 1]
sorted_arr, inversions = merge_sort(arr)
print(f"Sorted array: {sorted_arr}")
print(f"Number of inversions: {inversions}")

2. Data Structures

Array

3Sum, leetcode No.15, Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.固定i，然后用two pointers

def threeSum(self, nums: List[int]) -> List[List[int]]:
        res = []
        nums.sort()
        for i in range(len(nums)-2):
            if i > 0 and nums[i] == nums[i-1]:
                continue
            l, r = i+1, len(nums)-1
            while l < r:
                s = nums[i] + nums[l] + nums[r]
                if s < 0:
                    l +=1 
                elif s > 0:
                    r -= 1
                else:
                    res.append((nums[i], nums[l], nums[r]))
                    while l < r and nums[l] == nums[l+1]:
                        l += 1
                    while l < r and nums[r] == nums[r-1]:
                        r -= 1
                    l += 1; r -= 1
        return res

Heap / Priority queue

leetcode No.2542 maximum subsequence score: 输入 2个数组，选择 k 个 index，第一个数组对应 index 值的和乘以第二个数组对应 index 值的最小值，所能计算的最大的值；思路上就是对于第二个数组排序，注意需要降序

import heapq
class Solution:
    def maxScore(self, nums1: List[int], nums2: List[int], k: int) -> int:
        p = sorted([(v, m) for v, m in zip(nums1, nums2)], key=lambda x: -x[1])
        queue = []
        result = -1
        total = 0
        for pair in p:
            heapq.heappush(queue, pair[0])
            total += pair[0]
            if len(queue) > k:
                low = heapq.heappop(queue)
                total -= low
  
            if len(queue) == k:
                result = max(result, pair[1] * total)
  
        return result

Red-Black Trees

AVL Trees

Augmenting data structures

B-Trees

Disjoint sets (Union find)

Trie

class Trie:

    def __init__(self):
        self.s = {}

    def insert(self, word: str) -> None:
        tmp = self.s
        for v in word:
            if v not in tmp:
                tmp[v] = {}
            tmp = tmp[v]

        tmp["is_word"] = True

    def search(self, word: str) -> bool:
        tmp = self.s
        for v in word:
            if v in tmp:
                tmp = tmp[v]
            else:
                return False

        return "is_word" in tmp

    def startsWith(self, prefix: str) -> bool:
        tmp = self.s
        for v in prefix:
            if v in tmp:
                tmp = tmp[v]
            else:
                return False

        return True

Range query

Segment Tree

Fenwick tree (binary index tree)
用 O(n) 去 build，然后之后每次 update 和查询都是 O(log(n))
虽然说是 tree，但是直接使用 array 来实现也是非常容易

Linkedlist

to find if there is a cycle in a linked list

  class Node:
      def __init__(self, x):
          self.val = x
          self.next = None

  def is_cyclic(head):
      """
      :type head: Node
      :rtype: bool
      """
      if not head:
          return False
      runner = head
      walker = head
      while runner.next and runner.next.next:
          runner = runner.next.next
          walker = walker.next
          if runner == walker:
              return True
      return False

leetcode 25. Reverse Nodes in k-Group. Given a linked list, reverse the nodes of a linked list k at a time and return its modified list.

def reverseKGroup(self, head, k):
    dummy = jump = ListNode(0)
    dummy.next = l = r = head

    while True:
        count = 0
        while r and count < k:   # use r to locate the range
            r = r.next
            count += 1
        if count == k:  # if size k satisfied, reverse the inner linked list
            pre, cur = r, l
            for _ in range(k):
                cur.next, cur, pre = pre, cur.next, cur  # standard reversing
            jump.next, jump, l = pre, l, r  # connect two k-groups
        else:
            return dummy.next

3. Graph

A graph is simple if no edge starts and ends at the same node, and there are no multiple edges between two nodes
A graph is connected if there is a path between any two nodes
The connected parts of a graph are called its components
A graph is regular if the degree of every node is a constant d
In a coloring of a graph, each node is assigned a color so that no adjacent nodes

have the same color
A graph is bipartite if it is possible to color it using two colors.
A graph is bipartite exactly when it does not contain a cycle with an odd number of edges. 易知这么一个 cycle，依次染色最后是同色

Traverse

# 本质就是保存一个visited，然后遍历，dfs用stack，bfs用queue
def dfs_traverse(graph, start):
    visited, stack = set(), [start]
    while stack:
        node = stack.pop()
        visited.add(node)
        for nextNode in graph[node]:
            if nextNode not in visited:
                stack.append(nextNode)
    return visited

Topological sort

就是按照图中顺序，得到一个排序，DAG都有至少一个解，有环就没有解，一般的复杂度都是$O(

# Kahn's algorithm
def topo_sort(points, pre: Dict[str, set], suc: Dict[str, set]):
    order = []
    sources = [p for p in points if not pre[p]]
    while sources:
        s = sources.pop()
        order.append(s)
        for u in suc[s]:
            pre[u].remove(s)
            if not pre[u]:
                sources.append(u)
    return order if len(order) == len(points) else []


# 一个变种，calculate max latencies
# [('A', 'B', 100), ('A', 'C', 200), ('A', 'F', 100), ('B', 'D', 100),
#            ('D', 'E', 50), ('C', 'G', 300)]
# result = {'A': 500, 'B': 150, 'C': 300, 'D': 50, 'E': 0, 'F': 0, 'G': 0}
def topo_sort(latencies):
    source = set(i[1] for i in latencies)
    end = set(i[0] for i in latencies)

    next_nodes = defaultdict(set)
    prev_nodes = defaultdict(set)
    time_dict = dict()
    for n, prev, time in latencies:
        next_nodes[prev].add(n)
        prev_nodes[n].add(prev)
        time_dict[(n, prev)] = time

    node_results = defaultdict(int)

    topo_que = list(source - end)
    while topo_que:
        node = topo_que.pop()
        for v in next_nodes[node]:
            prev_nodes[v].remove(node)
            node_results[v] = max(node_results[node] + time_dict[(v, node)],
                                  node_results[v])
            if not prev_nodes[v]:
                topo_que.append(v)

    return node_results

Minimum spanning tree

Single-Source Shortest Paths

Dijkstra’s algorithm用于directed graph，而且edge weights $>= 0$
复杂度$O(E\log E+V)$

import heapq


def calculate_distances(graph, starting_vertex):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[starting_vertex] = 0

    pq = [(0, starting_vertex)]
    while len(pq) > 0:
        current_distance, current_vertex = heapq.heappop(pq)

        # Nodes can get added to the priority queue multiple times. We only
        # process a vertex the first time we remove it from the priority queue.
        if current_distance > distances[current_vertex]:
            continue

        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight

            # Only consider this new path if it's better than any path we've
            # already found.
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor))

    return distances

example_graph = {
    'U': {'V': 2, 'W': 5, 'X': 1},
    'V': {'U': 2, 'X': 2, 'W': 3},
    'W': {'V': 3, 'U': 5, 'X': 3, 'Y': 1, 'Z': 5},
    'X': {'U': 1, 'V': 2, 'W': 3, 'Y': 1},
    'Y': {'X': 1, 'W': 1, 'Z': 1},
    'Z': {'W': 5, 'Y': 1},
}
print(calculate_distances(example_graph, 'X'))
# => {'U': 1, 'W': 2, 'V': 2, 'Y': 1, 'X': 0, 'Z': 2}

All-Pairs Shortest Paths

Maximum flow

一个连通图，有s，t两个特殊的节点，其他节点都在s到t的某条path上
max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the total weight of the edges in the minimum cut, i.e. the smallest total weight of the edges which if removed would disconnect the source from the sink.
cut就是去掉一些edges，把s和t分开成两个图
capacity就是从s侧到t侧的容量和，注意不包括反向从t->s的那些edges的流量
max flow算法本质就是开始都是0，发现某path的最小处>0，那就加上这么小的流量填满。找path用dfs就是Ford-Fulkerson，用bfs就是 Edmonds–Karp

"""
Input : capacity, source, sink
Output : maximum flow from source to sink
Capacity is a two-dimensional array that is v*v.
capacity[i][j] implies the capacity of the edge from i to j.
If there is no edge from i to j, capacity[i][j] == 0.
"""
# current_flow刚开始设置很大的值，不断地随着dfs而变小
def dfs(capacity, flow, visit, vertices, idx, sink, current_flow = 1 << 63):
    # DFS function for ford_fulkerson algorithm.
    if idx == sink: 
        return current_flow
    visit[idx] = True
    for nxt in range(vertices):
        if not visit[nxt] and flow[idx][nxt] < capacity[idx][nxt]:
            tmp = dfs(capacity, flow, visit, vertices, nxt, sink, min(current_flow, capacity[idx][nxt]-flow[idx][nxt]))
            if tmp:
                flow[idx][nxt] += tmp
                flow[nxt][idx] -= tmp
                return tmp
    return 0

def ford_fulkerson(capacity, source, sink):
    # Computes maximum flow from source to sink using DFS. Greedy
    # Time Complexity : O(Ef) 也就是和edge还有max flow正比
    # E is the number of edges and f is the maximum flow in the graph.
    vertices = len(capacity)
    ret = 0
    flow = [[0]*vertices for i in range(vertices)]
    while True:
        visit = [False for i in range(vertices)]
        tmp = dfs(capacity, flow, visit, vertices, source, sink)
        if tmp: 
            ret += tmp
        else: 
            break
    return ret

4. Selected topics

4.1 Bit manipulation

# get largest power of 2 that <= n
n & -n

4.2 Dynamic programming

Using dynamic programming, it is often possible to change an iteration over permutations into an iteration over subsets complexity drop from $n!$ ->$2^n$
编辑距离

  # insert, delete or replace a character
  def minDistance(self, word1, word2):
      """Dynamic programming solution"""
      m = len(word1)
      n = len(word2)
      table = [[0] * (n + 1) for _ in range(m + 1)]

      for i in range(m + 1):
          table[i][0] = i
      for j in range(n + 1):
          table[0][j] = j

      for i in range(1, m + 1):
          for j in range(1, n + 1):
              if word1[i - 1] == word2[j - 1]:
                  table[i][j] = table[i - 1][j - 1]
              else:
                  table[i][j] = 1 + min(table[i - 1][j], table[i][j - 1],
                                        table[i - 1][j - 1])
      return table[-1][-1]

最长上升子序列

  def lengthOfLIS(self, nums: List[int]) -> int:
      if not nums:
          return 0
      dp = []
      for i in range(len(nums)):
          dp.append(1)
          for j in range(i):
              if nums[i] > nums[j]:
                  dp[i] = max(dp[i], dp[j] + 1)
      return max(dp)

最长公共子序列

  def longestCommonSubsequence(self, text1: str, text2: str) -> int:
      m, n = len(text1) + 1, len(text2) + 1
      s = [[0] * m for _ in range(n)]
      for i in range(1, n):
          for j in range(1, m):
              if text2[i - 1] == text1[j - 1]:
                  s[i][j] = s[i - 1][j - 1] + 1
              else:
                  s[i][j] = max(s[i - 1][j], s[i][j - 1])

      return s[-1][-1]

给定一个 int array，判断是否可以分成 2 个子 array，使得它们和相等

def can_split_into_two_equal_sums(nums):
    total_sum = sum(nums)

    # If total sum is odd, it's impossible to split into two equal sums
    if total_sum % 2 != 0:
        return False

    target_sum = total_sum // 2
    n = len(nums)
    dp = [[False] * (target_sum + 1) for _ in range(n + 1)]

    # Base case: If sum is 0, it's always possible (empty subset)
    for i in range(n + 1):
        dp[i][0] = True

    for i in range(1, n + 1):
        for j in range(1, target_sum + 1):
            if j < nums[i - 1]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]

    return dp[n][target_sum]

leetcode No.790 多米诺骨牌，有 2 种骨牌，对于 2 * n 的地面，有多少种全覆盖

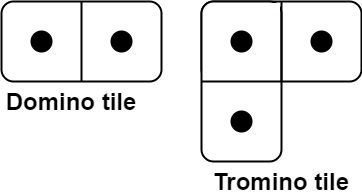
def numTilings(n: int) -> int:
        dp = [(1, 0, 0), (2, 1, 1)]
        for i in range(2, n):
            x = tuple([dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 2][0],
                       dp[i - 1][2] + dp[i-2][0], 
                       dp[i - 1][1] + dp[i-2][0]])
            dp.append(x)

        return dp[n - 1][0]

Linear programming

4.3 String matching

4.3.1 Rabin-Karp

4.4 Computational geometry

5. Miscellaneous

5.1 Parition of a number

partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers，不关心顺序

  # 这个是输出所有的partition结果
  def partitions(n, I=1):
      yield (n, )
      for i in range(I, n // 2 + 1):
          for p in partitions(n - i, i):
              yield (i, ) + p

  # 这个是计算有多少种分法，其实和上面的类似            
  def par(n, b=1):
      r = 1
      for i in range(b, n // 2 + 1):
          r += par(n - i, i)
      return r

5.2 Permutations & combinations

Derangement

A derangement (错排问题) is a permutation of the elements of a set, such that no element appears in its original position
下面是个简单的recursive的实现，比较优雅的是，$n = 0, 1$之类的情况也都包含了

from math import factorial


def selection(n, k):
    return factorial(n) // factorial(k) // factorial(n - k)


def derange(n):
    total = factorial(n)
    for i in range(1, n):
        total -= selection(n, i) * derange(n - i)

    return total - 1

还有一种动态规划的做法，很好理解。两种情况，要么n-1的排列没有原位的，要么有一个原位的（如果有$>=2$个，那么新加一个数换不过来）。就是对于$n-1$的情况来说，我新的这个数可以和derange(n-1)每一个情况中的任意一个位置互换，结果是valid的。除此之外，如果有一个数在original position，我和它互换可以使两个都错位

def derange(n):
    r = [0, 1]
    for i in range(3, n + 1):
        r.append((i - 1) * (r[-1] + r[-2]))

    return r[n - 1]

最后还有数学解法，derangements也叫subfactorial $!n$，有$!0=1,!1=0,!2=1$，https://en.wikipedia.org/wiki/Derangement
$!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}$
$\lim _{n\to \infty }{!n \over n!}={1 \over e}\approx 0.3679\ldots .$

import math


def derange(n):
    return round(factorial(n) / math.e)

5.3 Selection rank

similar to quick sort

5.4 Newton-Raphson algorithm

牛顿法就是按照公式更新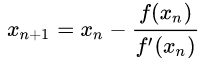，这里的公式说白了就是$x-r^{2}=0$，求它的解，第4行等价于r = r - (r**2 - x) / (2 * r)
如果满足$f^{\prime}(x)\neq0$, $f^{\prime\prime}(x)$ is continuous, $x_{0} $sufficiently close to the root，那么 rate of convergence is quadratic. https://en.wikipedia.org/wiki/Newton%27s_method#Failure_analysis

def sqrt(x):
    r = x
    while r * r > x:
        r = (r + x / r) / 2
    return r

5.5 Particle swarm optimization (PSO)

粒子群优化

for each particle i = 1, ..., S do
    Initialize the particle's position with a uniformly distributed random vector: xi ~ U(blo, bup)
    Initialize the particle's best known position to its initial position: pi ← xi
    if f(pi) < f(g) then
        update the swarm's best known position: g ← pi
    Initialize the particle's velocity: vi ~ U(-|bup-blo|, |bup-blo|)
while a termination criterion is not met do:
    for each particle i = 1, ..., S do
        for each dimension d = 1, ..., n do
            Pick random numbers: rp, rg ~ U(0,1)
            Update the particle's velocity: vi,d ← w vi,d + φp rp (pi,d-xi,d) + φg rg (gd-xi,d)
        Update the particle's position: xi ← xi + vi
        if f(xi) < f(pi) then
            Update the particle's best known position: pi ← xi
            if f(pi) < f(g) then
                Update the swarm's best known position: g ← pi

5.6 Walker’s alias method

一个根据 weights 生成随机数的方法
本质就是预处理weights，使得每个 bin 种只有 1 ～ 2个item，然后uniform random，把 binary search 变成了 constant 的查找
http://www-sop.inria.fr/members/Alain.Jean-Marie/Cours/AMM/Support/algos.pdf

5.7 Choice without repetition from numpy

n_uniq = 0
p = p.copy()
found = np.zeros(shape, dtype=np.int64)
flat_found = found.ravel()
while n_uniq < size:
    x = self.random((size - n_uniq, ))
    if n_uniq > 0:
        p[flat_found[0:n_uniq]] = 0
    cdf = np.cumsum(p)
    cdf /= cdf[-1]
    new = cdf.searchsorted(x, side='right')
    _, unique_indices = np.unique(new, return_index=True)
    unique_indices.sort()
    new = new.take(unique_indices)
    flat_found[n_uniq:n_uniq + new.size] = new
    n_uniq += new.size
idx = found

可以学习一下 numpy source code，这里就是分次生成一波一波的，然后把已经生成的 weights 设置成 0

To be continued …

Written on June 1, 2019